Trig-or-Treat
Law of Cosines

Definition:
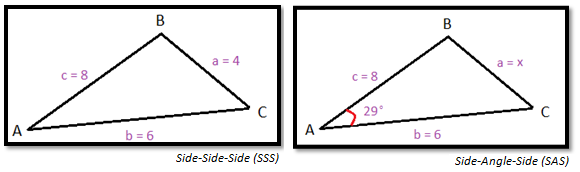
It is a law that relates the sides of any triangle to solve for its values. In other words, you could use the “Law of Cosines” to solve for non-right triangles when three sides (SSS) or a side, angle, and side (SAS) given.

Cases:










Objective:
• When given the values of all the sides of a non-right triangle, use Law of Cosines to find out the measurement of each side’s corresponding angles.
• When given the values of two sides and their included angle, use Law of Cosines to find out the value of the last side, and the measurement of the other two angles.

How To:
  • The lower case letters such as "a, b, and c" represents the labels for the triangle's sides.
  • The upper case letters such as "A, B, and C" represents the labels for the triangle's angles.
  • The same lower and upper case letter should correspond each other (ex. a and A). Side a should be opposite of angle A, so forth for the others.
  • Once you know that, all you have to do to solve for the triangle is plug in the given values into the formula.
  • Use your calculator to assist you.
*Formulas can be viewed here
If you want practice on L.O.C (Law of Cosines), check out the practice problems on the "extras" section of our website.
Law of Sines

Definition:
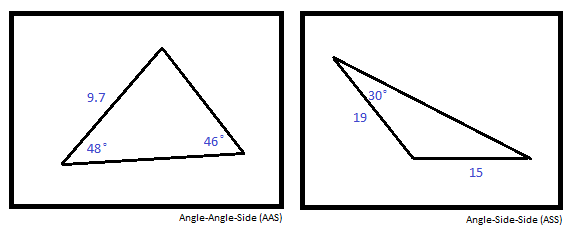
The Law of Sines is a ratio that relates any side of a triangle to its opposite angle. Similar to Law of Cosines, Law of Sines is used to solve for non-right triangles when a corresponding angle and side with an additional side or angle is given. In other words, Angle-Side-Side (ASS) or Angle-Angle-Side (AAS).

Cases:











Objective:
  • Use the Law of Sines to find the missing values of the non-right triangle.
  • Find out whether there will be 0, 1, or 2 solutions from solving the triangle. (Use the "Hinge Theorem")
Hinge Theorem:
  • States whether there are 0, 1, or 2 possible solutions when solving the triangle using Law of Sines.
  • Use the theorem when the problem gives you the values for ASS. 
  • Make one said be represented as r and the other side as h for height. Use theta as an example for your angle.
  • Knowing that the cases for the hinge theorem would be: if,


How To:
  • Some knowledge is required from knowing what each upper and lower letter represents. Refer to the Law of Cosines above this sections for more information.
  • Once you know that, use the Law of Sines: a/sin⁡a = b/sin⁡b = c/sin⁡c
  • Plug in given values already given to solve for the triangle
  • * Be aware there might be two possible solutions!
h = r sin theta          (there would be 1 solution)
h < r sin theta          (there would be no solutions)
h > r sine theta        (there would be 1 or 2 solutions)